4. Extras¶
Como a principal intenção do curso é prepará-los para o uso de SymPy nas disciplinas que envolvem Cálculo, ao finalizar o capítulo anterior você deve estar pronto para resolver seus problemas utilizando esse módulo. Contudo, eu acredito que há muito a se falar sobre esse módulo. E, portanto, esse capítulo fará uma abordagem rápida sobre algumas coisas que são possíveis com ele.
4.1. Geometria¶
Isso mesmo, nós podemos resolver problemas de Geometria tanto de forma simbólica, como de forma numérica. A ideia principal não é ficar criando plots com o sistema completo, mas sim trabalhar matemáticamente (indo para o lado da Geometria Analítica).
Antes de começarmos essa seção e as próximas, faremos as devidas importações e definições:
from sympy import *
from sympy.geometry import * # Importante garantir que foi importado corretamente
x, y, z = symbols('x y z')
init_printing(use_unicode=True, use_latex='mathjax')
2D¶
Começando pela geometria em 2D, podemos seguir o processo de criar os pontos, as linhas (a partir dos pontos) e as formas 2D a partir dos segmentos. É bem simples e intuitivo, veja:
O = Point(0,0)
A = Point(1,2)
B = Point(3,-4)
C = Point(-2, 3)
Você pode fazer as operações padrões entre pontos normalmente.
B - A ## AB
\[\displaystyle Point2D\left(2, -6\right)\]
Contudo, o indicado é utilizar as classes, que já terão suas propriedades a fácil acesso.
Segment(A,B) ## AB Simbólicamente
AC = Segment(A,C)
AC.slope ## inclinação
\[\displaystyle - \frac{1}{3}\]
AC.length ## comprimento
\[\displaystyle \sqrt{10}\]
AC.midpoint ## ponto médio
\[\displaystyle Point2D\left(- \frac{1}{2}, \frac{5}{2}\right)\]
AC.contains(A) ## Contém A?
\[\displaystyle \text{True}\]
AC.distance(B) ## Menor distância ao ponto B
\[\displaystyle 2 \sqrt{10}\]
Nós podemos criar linhas também
Line(A,B)
l1 = Line(A,B)
l1.equation() ## Equação da reta = 0
\[\displaystyle 6 x + 2 y - 10\]
l1.coefficients ## Coeficientes da reta
\[\displaystyle \left( 6, \ 2, \ -10\right)\]
Podemos criar uma reta ao dar um ponto inicial e uma inclinação, lembrando que: \(y - y_0 = m(x-x_0)\)
l2 = Line(C, slope = 3)
l2.equation()
\[\displaystyle - 3 x + y - 9\]
l3 = l2.perpendicular_line(A) ## Retorna uma reta perpendicular que passa pelo ponto dado
l3.equation()
\[\displaystyle - x - 3 y + 7\]
l3.slope # -m^-1
\[\displaystyle - \frac{1}{3}\]
E nós podemos ver a intersecção entre duas entidades geométricas.
intersection(l2,l3)
\[\displaystyle \left[ Point2D\left(-2, 3\right)\right]\]
intersection(l1, l3) # Ponto A
\[\displaystyle \left[ Point2D\left(1, 2\right)\right]\]
Para plotar, de modo geral, fazemos o uso do que aprendemos no último capítulo, a função plot_implicit.
plot_implicit(l1.equation())
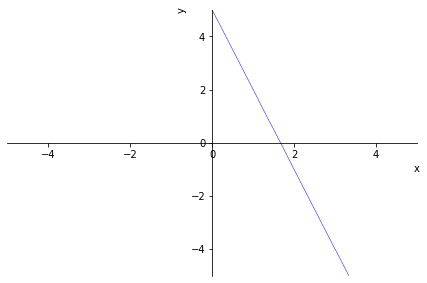
<sympy.plotting.plot.Plot at 0x7f9593fee1d0>
Podemos criar figuras geométricas e encontrar suas áreas e verficiar intersecções. Veja os exemplos:
trig = Triangle(A,B,C) # Cria um Triângulo
trig
trig.area ## Não utiliza valores absolutos
\[\displaystyle -8\]
abs(trig.area) ## Correto
\[\displaystyle 8\]
trig.perimeter ## Perímetro
\[\displaystyle \sqrt{74} + 3 \sqrt{10}\]
trig.orthocenter ## Centro Ortogonal
\[\displaystyle Point2D\left(\frac{25}{4}, \frac{23}{4}\right)\]
trig.circumcenter ## Circuncentro
\[\displaystyle Point2D\left(- \frac{17}{8}, - \frac{19}{8}\right)\]
trig.altitudes ## Alturas
\[\displaystyle \left\{ Point2D\left(-2, 3\right) : Segment2D\left(Point2D\left(-2, 3\right), Point2D\left(\frac{2}{5}, \frac{19}{5}\right)\right), \ Point2D\left(1, 2\right) : Segment2D\left(Point2D\left(1, 2\right), Point2D\left(- \frac{19}{37}, \frac{34}{37}\right)\right), \ Point2D\left(3, -4\right) : Segment2D\left(Point2D\left(3, -4\right), Point2D\left(\frac{23}{5}, \frac{4}{5}\right)\right)\right\}\]
trig.incircle ## Círculo interno
trig.incircle.equation()
\[\displaystyle \left(x - \frac{- \sqrt{10} + \sqrt{74}}{\sqrt{74} + 3 \sqrt{10}}\right)^{2} + \left(y - \frac{2 \left(\sqrt{10} + \sqrt{74}\right)}{\sqrt{74} + 3 \sqrt{10}}\right)^{2} - \frac{256}{\left(\sqrt{74} + 3 \sqrt{10}\right)^{2}}\]
trig.bisectors() ## Bissetrizes
\[\displaystyle \left\{ Point2D\left(-2, 3\right) : Segment2D\left(Point2D\left(-2, 3\right), Point2D\left(\frac{11}{16} + \frac{\sqrt{185}}{16}, \frac{47}{16} - \frac{3 \sqrt{185}}{16}\right)\right), \ Point2D\left(1, 2\right) : Segment2D\left(Point2D\left(1, 2\right), Point2D\left(- \frac{1}{3}, \frac{2}{3}\right)\right), \ Point2D\left(3, -4\right) : Segment2D\left(Point2D\left(3, -4\right), Point2D\left(\frac{77}{17} - \frac{6 \sqrt{185}}{17}, \frac{14}{17} + \frac{2 \sqrt{185}}{17}\right)\right)\right\}\]
trig.bisectors()[A] ## Bissetriz que passa no ponto A
trig.is_right() ## É triângulo retângulo?
False
trig.is_scalene() ## É triângulo escaleno?
True
circ = Circle(A, 3) ## Centro e Raio
circ
circ.equation()
\[\displaystyle \left(x - 1\right)^{2} + \left(y - 2\right)^{2} - 9\]
circ.circumference
\[\displaystyle 6 \pi\]
circ.area
\[\displaystyle 9 \pi\]
intersection(trig,circ)
\[\displaystyle \left[ Point2D\left(- \frac{19}{37} + \frac{5 \sqrt{410}}{74}, \frac{34}{37} - \frac{7 \sqrt{410}}{74}\right), \ Point2D\left(1 - \frac{9 \sqrt{10}}{10}, \frac{3 \sqrt{10}}{10} + 2\right), \ Point2D\left(\frac{3 \sqrt{10}}{10} + 1, 2 - \frac{9 \sqrt{10}}{10}\right), \ Point2D\left(- \frac{5 \sqrt{410}}{74} - \frac{19}{37}, \frac{34}{37} + \frac{7 \sqrt{410}}{74}\right)\right]\]
elips = Ellipse(B, 3, 2) ## Centro, Raio Horizontal, Raio Vertical
elips
elips.equation()
\[\displaystyle \left(\frac{x}{3} - 1\right)^{2} + \left(\frac{y}{2} + 2\right)^{2} - 1\]
elips.circumference ## Não há formulas
\[\displaystyle 12 E\left(\frac{5}{9}\right)\]
elips.circumference.evalf() ## Valor numérico
\[\displaystyle 15.8654395892906\]
elips.area
\[\displaystyle 6 \pi\]
elips.eccentricity
\[\displaystyle \frac{\sqrt{5}}{3}\]
elips.foci ## Focos
\[\displaystyle \left( Point2D\left(3 - \sqrt{5}, -4\right), \ Point2D\left(\sqrt{5} + 3, -4\right)\right)\]
elips.focus_distance ## Distância Focal
\[\displaystyle \sqrt{5}\]
D = Point(0,10)
quad = Polygon(A,B,C,D) ## Criando Polígono de N vértices
quad
abs(quad.area)
\[\displaystyle \frac{39}{2}\]
quad.angles
\[\displaystyle \left\{ Point2D\left(-2, 3\right) : - \operatorname{acos}{\left(- \frac{39 \sqrt{3922}}{3922} \right)} + 2 \pi, \ Point2D\left(0, 10\right) : - \operatorname{acos}{\left(\frac{54 \sqrt{3445}}{3445} \right)} + 2 \pi, \ Point2D\left(1, 2\right) : \operatorname{acos}{\left(- \frac{5 \sqrt{26}}{26} \right)}, \ Point2D\left(3, -4\right) : - \operatorname{acos}{\left(\frac{13 \sqrt{185}}{185} \right)} + 2 \pi\right\}\]
quad.angles[A] ## No ponto A
\[\displaystyle \operatorname{acos}{\left(- \frac{5 \sqrt{26}}{26} \right)}\]
from sympy.physics.units import degree ## Importação das unidades
(quad.angles[A]/degree.scale_factor).evalf() ## Transforma em Graus
\[\displaystyle 168.69006752598\]
reg = RegularPolygon(A,1,4) # Centro, Raio, Qtd. Lados
reg
reg.angles # Retângulo
\[\displaystyle \left\{ Point2D\left(0, 2\right) : \frac{\pi}{2}, \ Point2D\left(1, 1\right) : \frac{\pi}{2}, \ Point2D\left(1, 3\right) : \frac{\pi}{2}, \ Point2D\left(2, 2\right) : \frac{\pi}{2}\right\}\]
reg.vertices # Vértices
\[\displaystyle \left[ Point2D\left(2, 2\right), \ Point2D\left(1, 3\right), \ Point2D\left(0, 2\right), \ Point2D\left(1, 1\right)\right]\]
Para finalizar com a Geometria, é importante relembrar que é possível fazer tudo isso com valores simbólicos. Por exemplo, um quadrado em função de um lado \(x\):
sim_quad = Polygon(Point(x/2, x/2), Point(-x/2, x/2),Point(-x/2, -x/2),Point(x/2, -x/2))
sim_quad
\[\displaystyle Polygon\left(Point2D\left(\frac{x}{2}, \frac{x}{2}\right), Point2D\left(- \frac{x}{2}, \frac{x}{2}\right), Point2D\left(- \frac{x}{2}, - \frac{x}{2}\right), Point2D\left(\frac{x}{2}, - \frac{x}{2}\right)\right)\]
sim_quad.area
\[\displaystyle x^{2}\]
3D¶
Para a terceira dimensão, podemos utilizar os Pontos com três coordenadas para gerar nossas formas.
M = Point(1, 2, 3)
N = Point(-2, 3, 4)
P = Point(5, -8, 10)
Line(M,N)
\[\displaystyle Line3D\left(Point3D\left(1, 2, 3\right), Point3D\left(-2, 3, 4\right)\right)\]
Line(M,N).equation()
\[\displaystyle \left( x + 3 y - 7, \ x + 3 z - 10\right)\]
Plane(M,N,P) # Plano
\[\displaystyle Plane\left(Point3D\left(1, 2, 3\right), \left( 17, \ 25, \ 26\right)\right)\]
Plane(M,N,P).equation()
\[\displaystyle 17 x + 25 y + 26 z - 145\]
4.2. Reações em Vigas (Mecânica)¶
Nós podemos analisar as tensões em vigas utilizando o sympy.physics.continuum_mechanics. Caso você procure aplicar carregamento em uma viga e então avaliar as reações e seus gráficos, certamente isso vai te auxiliar.
Veja um exemplo (no caso, para fazer sentido, leva os mesmos valores de um exemplo da documentação):
from sympy.physics.continuum_mechanics.beam import Beam
E, I = symbols('E I') ## Símbolos para o Módulo de Elasticidade e o Momento de Inércia
R1, R2 = symbols('R1 R2') ## Símbolos para as forças
b = Beam(50, 20, 30) ## Criando a viga (comprimento, E, I)
b.apply_load(R1, 0, -1) ## Aplicando carregamentos (intensidade, início, ordem)
###
### Momentos, order = -2
### Forças Pontuais, order =-1
### Forças distribuídas linearmente, order = 0
### Veja os outros na documentação
###
b.apply_load(R1, 10, -1)
b.apply_load(R2, 30, -1)
b.apply_load(90, 5, 0, 23)
b.apply_load(10, 30, 1, 50)
b.load ## Carregamento
\[\displaystyle R_{1} {\left\langle x \right\rangle}^{-1} + R_{1} {\left\langle x - 10 \right\rangle}^{-1} + R_{2} {\left\langle x - 30 \right\rangle}^{-1} + 90 {\left\langle x - 5 \right\rangle}^{0} - 90 {\left\langle x - 23 \right\rangle}^{0} + 10 {\left\langle x - 30 \right\rangle}^{1} - 200 {\left\langle x - 50 \right\rangle}^{0} - 10 {\left\langle x - 50 \right\rangle}^{1}\]
b.shear_force() ## Força Cortante
\[\displaystyle - M_{0} {\left\langle x \right\rangle}^{-1} - R_{0} {\left\langle x \right\rangle}^{0} - R_{20} {\left\langle x - 20 \right\rangle}^{0} - R_{50} {\left\langle x - 50 \right\rangle}^{0} - \frac{224 {\left\langle x \right\rangle}^{0}}{15} - 90 {\left\langle x - 5 \right\rangle}^{1} - \frac{224 {\left\langle x - 10 \right\rangle}^{0}}{15} + 90 {\left\langle x - 23 \right\rangle}^{1} + \frac{54748 {\left\langle x - 30 \right\rangle}^{0}}{15} - 5 {\left\langle x - 30 \right\rangle}^{2} + 200 {\left\langle x - 50 \right\rangle}^{1} + 5 {\left\langle x - 50 \right\rangle}^{2}\]
b.bending_moment() ## Momento Fletor
\[\displaystyle - M_{0} {\left\langle x \right\rangle}^{0} - R_{0} {\left\langle x \right\rangle}^{1} - R_{20} {\left\langle x - 20 \right\rangle}^{1} - R_{50} {\left\langle x - 50 \right\rangle}^{1} - \frac{224 {\left\langle x \right\rangle}^{1}}{15} - 45 {\left\langle x - 5 \right\rangle}^{2} - \frac{224 {\left\langle x - 10 \right\rangle}^{1}}{15} + 45 {\left\langle x - 23 \right\rangle}^{2} + \frac{54748 {\left\langle x - 30 \right\rangle}^{1}}{15} - \frac{5 {\left\langle x - 30 \right\rangle}^{3}}{3} + 100 {\left\langle x - 50 \right\rangle}^{2} + \frac{5 {\left\langle x - 50 \right\rangle}^{3}}{3}\]
p = b.draw()
p.show() ## Ilustração Gráfica
b.solve_for_reaction_loads(R1, R2) ## Solucionando
b.plot_bending_moment() ## Plot Momento Fletor
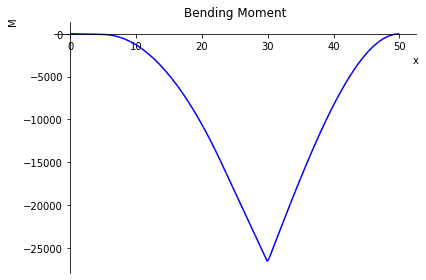
<sympy.plotting.plot.Plot at 0x7f9576b37cd0>
b.plot_shear_force() ## Plotando Força Cortante
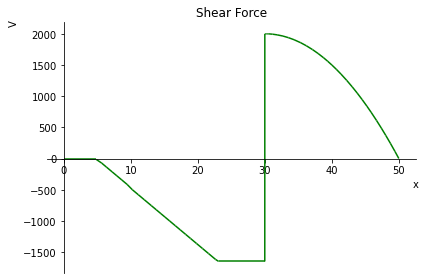
<sympy.plotting.plot.Plot at 0x7f9576c90d50>
b.apply_support(50, 'pin') ## Criando apoios
b.apply_support(0, 'fixed')
b.apply_support(20, 'roller')
b.load
\[\displaystyle M_{0} {\left\langle x \right\rangle}^{-2} + R_{0} {\left\langle x \right\rangle}^{-1} + R_{20} {\left\langle x - 20 \right\rangle}^{-1} + R_{50} {\left\langle x - 50 \right\rangle}^{-1} + \frac{224 {\left\langle x \right\rangle}^{-1}}{15} + 90 {\left\langle x - 5 \right\rangle}^{0} + \frac{224 {\left\langle x - 10 \right\rangle}^{-1}}{15} - 90 {\left\langle x - 23 \right\rangle}^{0} - \frac{54748 {\left\langle x - 30 \right\rangle}^{-1}}{15} + 10 {\left\langle x - 30 \right\rangle}^{1} - 200 {\left\langle x - 50 \right\rangle}^{0} - 10 {\left\langle x - 50 \right\rangle}^{1}\]
p = b.draw()
p.show()
